Fomaspeed gyártói adatok.
|
A hullámhossz, fókusztáv és lukátmérő összefüggései
Az ábrán jól látszik, hogy kb. 475nm hullámhosszra a legérzékenyebb a papír, 550 nanométernél már egyáltalán nem érzékeny, és az ennél hosszabb hullámokra is vak (ezért dolgozhatunk vele vörös biciklilámpa fényében).
Az ábrán jól látszik, hogy kb. 475nm hullámhosszra a legérzékenyebb a papír, 550 nanométernél már egyáltalán nem érzékeny, és az ennél hosszabb hullámokra is vak (ezért dolgozhatunk vele vörös biciklilámpa fényében).
Ennek azért van jelentősége, mert a Pinhole designer alapértelmezetten 0,00055 milliméterben átlagolja a fény hullámhosszát. Ennek megfelelően ajánl adott lukátmérőhöz fókusztávolságot. Azonban ha 0,00047-el számolunk, egy 0,27mm lukhoz már nem 36mm, hanem 43mm fókusztávolság az ideális.
Persze, amikor döföd a tűt, nem kérdezed mennyire lesz ideális az a luk, és mekkora fókusztáv jár hozzá, de ha valaki profi lukat vásárol, akkor már ad a részletekre is. Miért is?
Már volt szó róla, hogy a kész képen 0,2mm CoC egy elfogadható érték (25 centiről nézve a képet). A cél tehát az, hogy olyan lukkamerát építsünk, amelyik szóródási köre ezt nem haladja meg. Erre egy képlet:
Airy Disk = 2 * 1.22 * lambda * ( f / D ), ahol: lambda = hullámhossz (mm), f = fókusztávolság (mm), D = lukátmérő (mm)
Tehát 2*1,22*0,00047*(50/0,27) =0.21mm. Hát éppen csak hogy :) De ha mondjuk 550 nanométerrel számolnánk, máris 0,25 lesz a szóródási kör, ami már határesetnek sem nevezhető. Amennyiben a fókusztávolságot a Pinhole Designer által javasolt 43 milliméterre alakítanánk, a szóródási kör több mint ideális 0,18mm lenne. Szóval a lukkamera képének élessége nanométereken múlik!
Az exponálási idő meghatározása
A Schwarzschild effektusról fotópapírra semmilyen adatot nem találtam, a fórumokon mindenfélét bölcsködnek, mindenesetre verőfényes napon 30-60 másodperc nagyjából mindenhol felmerül, a kompenzáció úgyis csak a hosszabb idők esetén jönne számításba (vagy ez volna a határeset).
Már volt szó róla, hogy a kész képen 0,2mm CoC egy elfogadható érték (25 centiről nézve a képet). A cél tehát az, hogy olyan lukkamerát építsünk, amelyik szóródási köre ezt nem haladja meg. Erre egy képlet:
Airy Disk = 2 * 1.22 * lambda * ( f / D ), ahol: lambda = hullámhossz (mm), f = fókusztávolság (mm), D = lukátmérő (mm)
Tehát 2*1,22*0,00047*(50/0,27) =0.21mm. Hát éppen csak hogy :) De ha mondjuk 550 nanométerrel számolnánk, máris 0,25 lesz a szóródási kör, ami már határesetnek sem nevezhető. Amennyiben a fókusztávolságot a Pinhole Designer által javasolt 43 milliméterre alakítanánk, a szóródási kör több mint ideális 0,18mm lenne. Szóval a lukkamera képének élessége nanométereken múlik!
Az exponálási idő meghatározása
A Schwarzschild effektusról fotópapírra semmilyen adatot nem találtam, a fórumokon mindenfélét bölcsködnek, mindenesetre verőfényes napon 30-60 másodperc nagyjából mindenhol felmerül, a kompenzáció úgyis csak a hosszabb idők esetén jönne számításba (vagy ez volna a határeset).
Tehát hogyan jön ki ez a kiindulási exponálási érték, ami aztán empirikusan finomítható? Mivel a szűk rekeszértékekben az interneten nincsen konszenzus (f/64 fölött már hatalmas a szórás a szakirodalomban), ezért mi most ezt használjuk:
Tehát valami ilyesmi sorozatot kapunk: 1, 1.4, 2, 2.8, 4, 5.6, 8, 11, 16, 22, 32, 45, 64, 90, 128, 181, 256, 362
Apertúránk pedig, fokális táv / luk mérete, 50mm/0,27mm = kb. f/185-ös rekesz, ami nagyjából 6 teljes rekesznyire van az f/22-től, ami még kimérhető az átlag fénymérőkkel.
Ehhez kell számítani a papír érzékenységét, ami hosszas keresgélések után sem került meg (mindenki mindenfélét állít mindenféle nyersanyagokról), mindenesetre filmes érzékenységi értékben számítva kb ISO 5 egy jó kiindulási alap lehet. (A fenti táblázat értékei nem analógok a film ISO értékeivel.) Ez tehát még újabb 5 EV-t ad hozzá a fénymérő által ISO200-on mért értékből.
Összesen tehát fénymérővel ISO200, f/22 mellett mért záridőt kb. 10-11 EV-nek megfelelő idővel kell kompenzálni. Így napsütésben 1-2 perc exponálási idő jönne ki.
De ha biztosra akarsz menni, akkor a legjobb, ha megkérdezed Csabát, ő mennyit exponálna :)

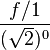


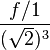
szédületes végig olvasni a sok szám/szám-ot,de rá is jöttem ha tudnám a választ lehet nem lyukkameráznék, hanem lyukakat árulnék lyukkamerákhoz. lyukkamérával- legyen szó 9*13 cm, vagy 24*30 cm-es negatívról akkor tettszik igazán az eredmény, ha Napsütésben egy perc körűl exponálok a mostanában gyártott fotópapírokra. minden új csomag fotó papírt egyszer BELÖVÖK, azután számolok.
VálaszTörlésvalahogy így= 1perc Napon, délben,-esőben ugyancsak délben 11 perc.
a százas csomag 80%-a sikeresen ki van exponálva