Rozé - Geogebra kalandok

Nem tudjuk, hogy pontosan mit csinálunk, há' me' matematikusok sem vagyunk, de rohadtul élvezzük. Szóval van itt ez a matematikai rozé, amitől pont részegülünk. 

Forrás: wiki

Ugyanennek az ábrának a bővebb kiadása meg itt található. A témakörre meg van egy remek előadássorozat is (karteziánus meg poláris koordinátákról és ezekről a csudi figurákról). 

A cuccot így kell elképzelni poláris koordináta rendszerben:

r=a*cos(b*Θ)     (vagy 90 fokban elforgatva: r=a*sin(b*Θ) - de ezzel most ne bonyolítsunk)

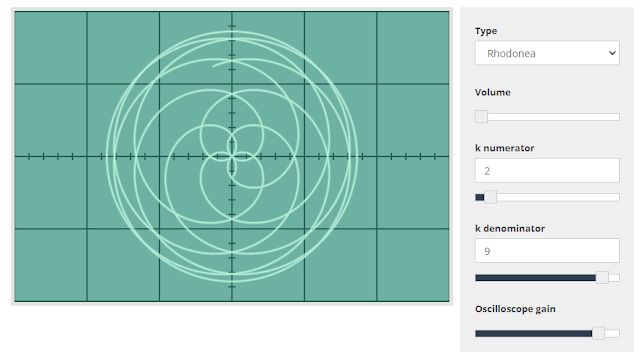
Ahol egy pont koordinátáját úgy adjuk meg, hogy r az origótól való távolság (sugár), a Θ pedig a vízszintestől (vagy elforgatva 90 fokban, a második esetben a függőleges tengelytől) való eltérés szöge. Az a  pedig a szirmok hegyének távolsága az origótól, vagyis a szirmok amplitúdója vagy mije, legnagyobb kitérése, ez az alábbi ábrán maximum 5 lehet. Gyakorlatilag ez csak a rózsa méretét befolyásolja. A b pedig a fenti ábrának az n/d értéke (n-numerator, d-denominator). A P-vel jelzett ponttól körben a szirmok csúcsai sorrendben számozva vannak, így végigkövethető a rajzolat. Tehát minden egyes szögnek (iránynak) a vízszintestől megfelel egy r hosszúság, ami a szögeket változtatva (0 és 2Pi között vesz fel értéket) leírja az alábbi ábrát:

Szimulátor

b egész(!) páros szám esetén az origóból eredő szirmok keletkeznek, ezek száma 2*b, b egész (!) páratlan esetén a szirmok száma b. 

Sajnos ezzel az eszközzel b-re csak egész számokat lehet beállítani, nekünk viszont a táblázat összes krikszkraksza (egyes formáknak külön nevük is van) kell, azok is, amikre b=n/d nem egész szám.  Ha b nem egész szám, akkor azok speciális esetek.

Forrás

Mindenesetre a fenti rózsa-táblázatban látszik egy mintázat, például az 1/3 ugyanazt eredményezi, mint a 2/6, vagy a 2/1 ugyanaz, mint a 8/4, stb. Az n és a d arányt valahogy így kell elképzelni, ha már feltétlenül el kell képzelni:

A wikin van még hasonló (n/d=3, a kék vonal meg az a, vagyis a szirom hossza)

Vagy így is el lehet képzelni:

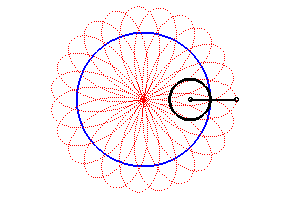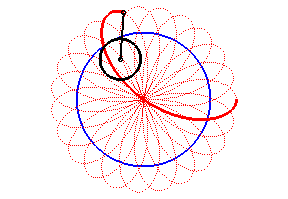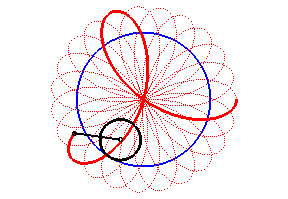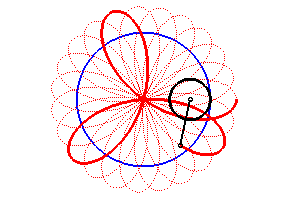Forrás

De ha ebbe a szimulátorba bemásolod ezt a függvényt: 10cos(bθ)  dom=(0, cπ)
ahol b helyére bármilyen számot írhatsz, és a c értékét szükség szerűen növeled, akkor leanimálhatod  magadnak az összeset.

Próbáljuk körbenyalogatni, hogyan lehetne ezekre az ábrákra szimulációt találni, a Win10 Calculator Graphingjába beletörött a bicskánk. A továbbiakban a Geogebrával folytatjuk. Legalább kicsit gyakoroljuk, hogyan működik a Geogebra függvényszerkesztője, amit csak alig nehezít az a tény, hogy a matekhez se értünk. Bár úgy tűnik, ez karteziánus koordináta, mégis remekül működik az r=cos(b*Θ) képlettel. A képletből kihagyjuk az a-t, ez egység lesz, a b értékét pedig az n és a d értékén keresztül változtatjuk. 

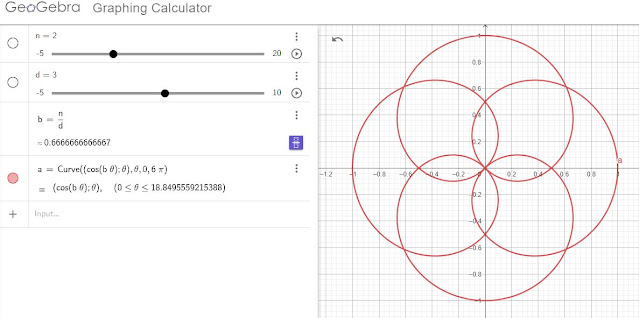
b=1 esetén (páratlan szám) b számú vagyis egyetlen szirmot kapunk, vagyis egy sima kört. Ez egy fél ciklus 0-Pi között.

b=2 , vagyis páros szám esetén 4 szirmot kapunk (pozitív és negatív félciklusokból) azonban csak két teljes ciklusban (2Pi alatt) lehet kirajzolni:

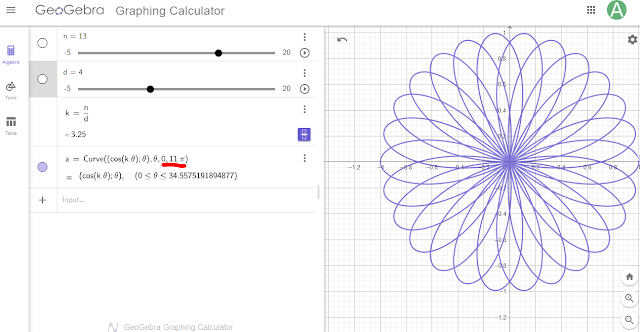
Míg a b=1 esetekben elég 0-és Pi közötti érték, addig a komplexebb ábrákhoz nagyobb értelmezési tartomány, vagy micsoda kell, de nem jöttünk rá hogy pl a 18/7-es aránynál pontosan hogyan kellene megjósolni, hogy hány periódusban tudja végig rajzolni a teljes krikszkrakszot. 

Mindenesetre addig tweakelgettük, hogy teljesen le tudtuk fedni a jasondavies táblázatot. Ehhez kellően nagy értelmezési tartományt kell adni a Θ szögnek (az ábra szempontjából teljesen mindegy hogy -9Pi, +9Pi, vagy 0, 18Pi).

Na jó, ha valaki nem akar monyolni a Geogebrával, annak itt van ez az academo szimulátor. Pont ezt csinálja.

Forrás