
 |
| A kvantált DCT |
-26 -3 0 -3 -3 -6 2 4 1 -4 1 1 5 1 2 -1 1 -1 2 0 0 0 0 0 -1 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
A DC értéket amúgy az előző blokkhoz viszonyítva bonyolultabbul menthetik, arra alapozva, hogy a szomszédos blokkok átlagai közel esnek egymáshoz, inkább a kis méreten kódolható eltérést kódolják, mint a nagydinamikájú adatot, ebbe most nem megyünk bele.
Na innen kezdve aztán elég sokféleképpen magyaráz az internet. A futamhossz-kódolást (run-lenght-encode) többnyire szöveggel és karaktereinek kódolásával mutatják be, de volt aki nem átallotta almákkal és banánokkal. Na midegy, mi képpel dolgozunk. Azt a módszert vesszük át, amit a leghitelesebbnek ítéltünk meg (8 perc környékén tér rá erre Amir úr).
A futáshossz-kódolás (RLE) lényege, hogy az egymást követő azonos értékeket pl. zérósok (más weboldalakon, videókban minden ismétlődő érték), ne fogyasszanak sok tárhelyet. Csökkentjük a redundanciát, de mi most csak a nullásokkal (azér' kvantáltunk, hogy jó sok legyen), olyan formában, hogy megadjuk a zérósok számát (r), majd az azokat követő AC érték tárolására szükséges bitek számát (s) - innen fogja tudni a kiolvasó program, hogy pontosan mit kell kiolvasni, mint AC adatot, majd magát a zérósokat követő AC értéket magát (c).
[(r,s),c]
Tehát a sorunk elemein végighaladva:-26 -3 0 -3 -3 -6 2 4 1 -4 1 1 5 1 2 -1 1 -1 2 0 0 0 0 0 -1 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[(0,5),-26] - mivel a DC az első elem, ezért itt az r=0, és máris belefutottunk Amir Nagah videójában egy érdekességre. Ő azt állítja, hogy -26 elkódolható s=5 biten. Felmerült bennem, hogy a negatív előjellel meg mi van? Írtam is neki kérdés-kommentet, lám mit válaszol.
[(0,2),-3] - a második érték előtt sincs zérós, -3 meg Amir szerint 2 biten tárolható. Egyelőre ezzel tárhelyet pazarlunk, de nézzük a zöld zónát:
[(5,1),-1] - 5 zérós előzi meg a -1-et. Itt már 3 számmal írtunk le ötöt, de az igazán érdekes az a feketével kiemelt sor:
[(0,0)] - ez az EOB jel, ha az r és az s is nullás, akkor innentől a blokk végéig mind zérós jön. Na itt történik a nagy redundanciacsökkentés és tömörítés.
Amir a videójában azt állítja, hogy a JPEG-ben minden (r,s) párost egyetlen byte ír le, amiből a felső négy bit az r, az alsó négy bit az s. Amennyiben az r nem elég (a zérósok száma >15), több rövidebb futamhossz-kódolásból oldják meg. Az s értékére max. 11-et ír (15 helyett), ennek köze lehet a fent említett előjel-problémának a megoldásához (lássuk mit válaszol). 11 biten mellesleg 2047-ig kódolhatunk. Gyakorlatilag tehát az történik, hogy 15 nullást egyetlen byte kódolhat el. Az EOB byte meg bármennyi nullást.
Egy valós képen, ahol a 8*8-as blokkok homogének és nagyobb felületeken sem nagyon ütnek el egymástól (pl. a fél képen kék ég húzódik), egyes (r,s) párosok sokkal gyakrabban fognak előfordulni, mint mások. Tehát ha a [(r,s),c] sorozatokat egymás után fűzzük (binárisan persze), akkor lesznek benne patternek, amelyek gyakran fordulnak elő, mások kevésbé. Ezeket érdemes helyettesíteni, a gyakoriakat rövidebb szimbólummal, a ritkábbakat hosszabbal, így további tárhely spórolható meg.
Ezt csinálja a Huffman kódolás (ebből is többféle van), bár létezik JPEG-ben aritmetikai kódolás is, ami még nagyobb tömörítést eredményez, viszont macerásabb (talán a JP2000, de arra a körhintára nem kívánunk felülni). Lényege az, hogy az elkódolni kívánt elemeket statisztikai gyakoriságuk szerint rendezi, a kevésbé gyakori elemekhez rendel nagyobb címet, a gyakoriakat pedig kevés biten kódolja. A youtube tele van magyarázatokkal, ne spóroljátok meg. Én sem írnám le jobban. Ezt a tömörítést az interneten általában szövegkódolással illusztrálják, tegyünk így mi is, egy Eminem nótában pl. a fuck szó lenne a legrövidebben megcímezve, a hegeli dialektika pedig a leghosszabban (de lehet, hogy tévedek és ilyet egyszer se mondott ki). Tipikus programozói feladat. Azért egy képernyőképet ideszúrok magamnak emlékeztetőnek. Az a1, a2 stb. a kódolni kívánt elemek, pirossal az előfordulásuk gyakorisága jelenik meg. Sárga mezőben pedig az elkódolásukhoz szükséges bináris cím.
Az így keletkezett címeket egymás után írjuk. A legszebb ebben a trükkben az, hogy míg a szavakat szóközök jelzik, a morzéban meg pl. szünet vezeti be a következő jelet, itt a teljes hosszú bit-kolbászban nincs szükség elválasztó szimbólumokra az egyes jelek között, maga a kiolvasási rendszer garantálja a helyes visszakódolást:
például legyen ez a Huffman-kódolt bitstream: 010110101010011101001011101010110010101010
A fenti bináris fa segítségével sorban kiolvassuk. A színek jelzik, melyik szimbólumot melyik szakaszból vesszük: a1, a2, a3, a2, a2, a2, a1, a4, a1, a2, a1, és így tovább, egyszerűen nem lehet másképp kiolvasni.
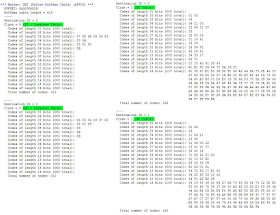
Minden képnek saját bináris fája van, természetesen a visszafejtéshez a JPEG filenak tartalmaznia kell az adott adathalmaz visszafejtéséhez szükséges információkat. A Huffman-kódot is lehet tweakelni a haladóbbaknak, a jobb eredmény érdekében. Mi azonban csak tátjuk a szánkat, a JPEGsnoppal ilyesmiket találtunk Huffman kulcsszóra a tesztekhez használt képünkben:
Mivel a százalék értékek nem pontosak, csak a nagyságrend számolható ki, a négy tábla összes adata megegyezik a 12 megapixeles kép összes pixeleinek a számával. Eben az esetben a DC táblázatban az látszik, hogy a leggyakoribb adatokat 3 biten kódolja, de találtunk olyan képet is, amiben már 1 biten. Gondolom ez azon múlik, milyen bináris fát sikerül létrehozni (levél-ág, vagy ág-ág szerkezet van a gyökér után).
A tömörítésben még van egy fontos tényező, a subsampling, de mivel azt nem mindig alkalmazzák, külön tárgyaljuk a következő részben. Nagyjából ennyi volt a JPEG elkódolása, megnyitáskor pedig ugyanezek a folyamatok fordítva játszódnak le. Ennyike.


ertem en hogy erted, de ha egy laikus megkerdi hogy ez gyakorlatban mire jo, akkor mi a tomondatos valasz?
VálaszTörlésHúha, tőmondatban nem tudok válaszolni. Számomra nosztalgiát ébreszt majd húsz évvel ezelőtti programozás órák iránt. Mármint a futam meg a Huffman. Azonkívül fitnesz az agynak. De ha az összes JPEG posztra gondolsz, akkor egy csomó jó játékra ad lehetőséget, pl. megértek olyan cikkeket, amelyek a képi beavatkozás felderítéséről szólnak, és ha nem is tudnám utána leprogramozni ennyi tudással még, de legalább megértem a logikáját néhány szoftvernek, pl. szteganográfia, vagy hibrid-képek. Aztán választ lehet kapni arra, hogy mennyire veszteségesen ment a Nikon. Hányszor és milyen minőségekben érdemes/lehet újramenteni egy JPEG-et. Pl. tudtad, hogy egy 10-es minőségre mentett JPEG rosszabb lehet, ha 12-esnek mented? Vagy a 7-es tutti rosszabb, mint a 6-os? Hogy kell e az optimized pipa vagy fölösleges? Aztán, hogy hány biten érdemes bizonyos műveleteket elvégezni, vagy veszteséges e egy sima JPEG elforgatás. Más fileformátumokkal is csak úgy lehet összehasonlítani, ha értjük hogyan működnek. Most hirtelen ennyi jut eszembe. Persze ettől még nem készülnek jó fotók. De az egy teljesen más témakör. És, hogy más mire tudja használni ezt a gyakorlatban? Azt nekem nem kell tudnom, mert ez egy egó-napló, nem tanfolyam :)
VálaszTörlés