Gitárom pengetem... a kék-veres hullámokat lengetem.

A zene és azon belül a gitározás megértéséhez nem tudtuk kikerülni az állóhullámok témakörét. Mármint a húrokban. Pedig megpróbáltuk. Tehát, a pengetéstől a hullám elindul kétfelé, a húr anyagának, tömegének és feszességének megfelelő valamilyen sebességgel, a nyak és a híd irányába, onnan visszaverődik a két tranzverzális hullám, valahol találkoznak önmagukkal, interferálnak és addig jönnek-mennek a két fix pont között, amíg egyes helyeken kierősítik, máshol kioltják egymás hatását és végül állóhullám lesz belőlük. Valahogy így.

Forrás

De ne tévesszen meg senkit, ezek a hullámok, amiket kamerával rögzítenek a gitár húrjairól nem azok a hullámok. 

Ezek a rezgő húr mozgásának és a kamera soronkénti képkiolvasásának közös szüleményei, vagyis artifaktjai. Látványosak, de félrevezetőek. Kicsit bővebben, és a youtubon szokásos ripacskodással fűszerezve, itt magyarázzák el az alapokat. Itt meg a longitudinális hullámokat. 

Ugyanis számunkra sokáig komoly akadályt jelentett a megértésben az, hogy a hang hullámformája, amit pl. Audacityben ábrázolunk, hasonlít a rezgő húr alakjához. Emiatt az volt a képzetünk, hogy a húr olyasmi mozgást ír le, mint az általa keltett hang ábrázolása. Pedig inkább így kell elképzelni:

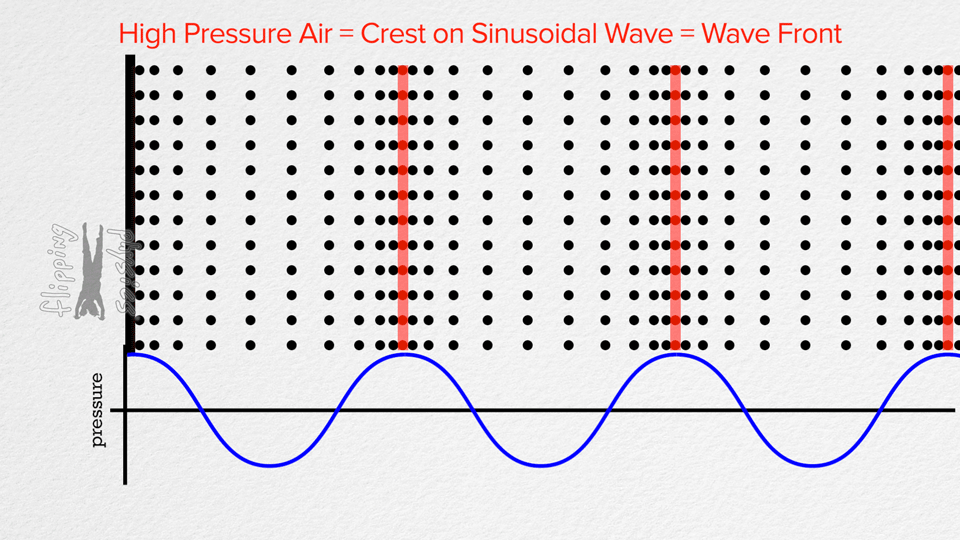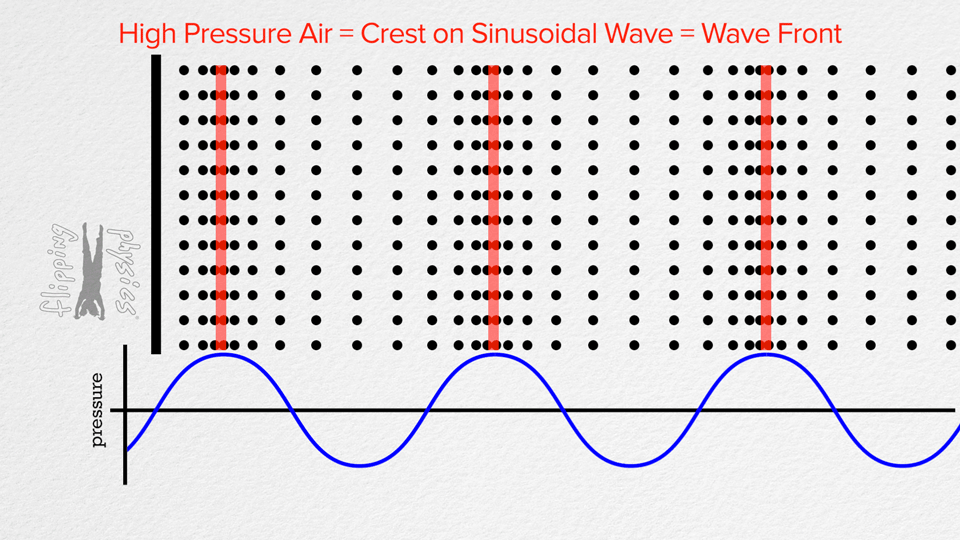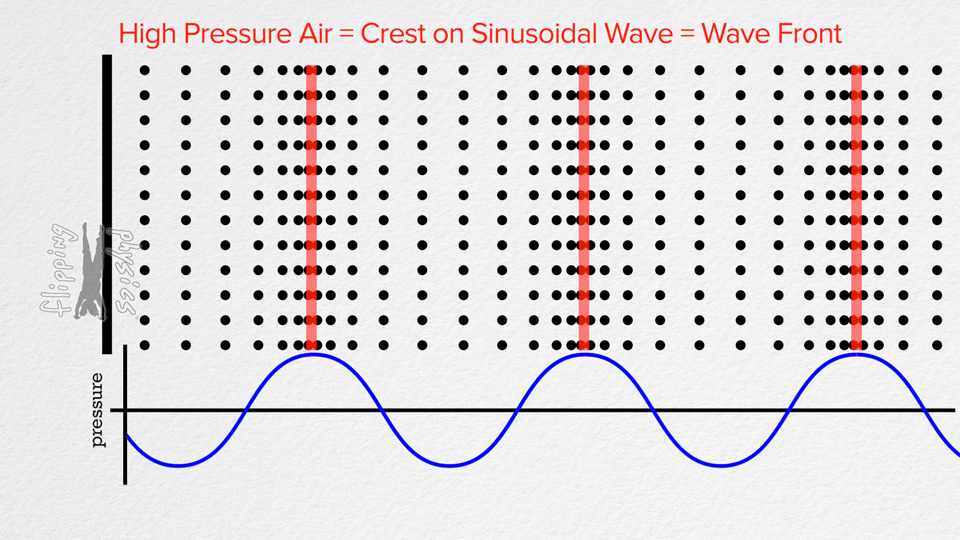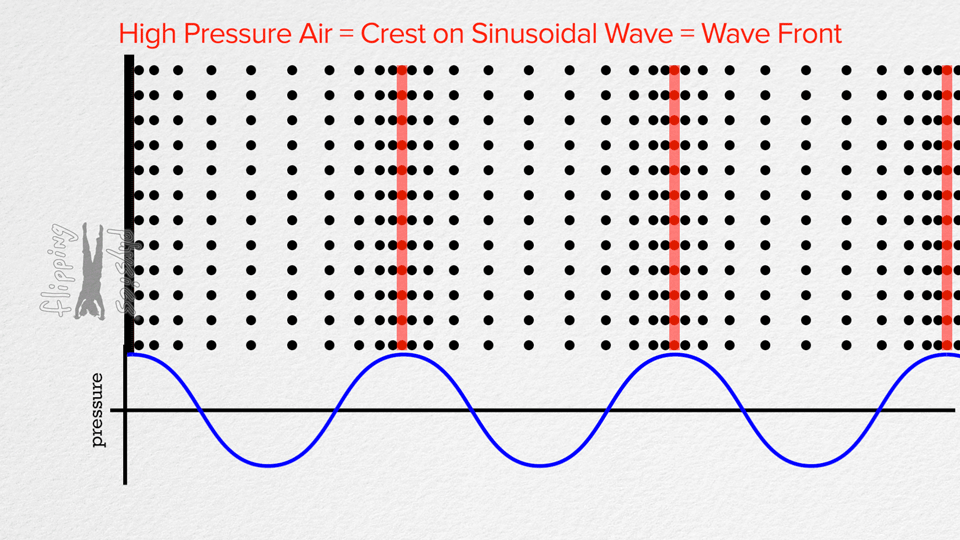Forrás

Az ábra bal oldalán a húr mozog oldalirányban (transzverz). A levegőben viszont longitudinálisan halad a hullám. A húr rezgési frekvenciája megegyezik a levegőben terjedő hang frekvenciájával (hiszen a húr mozgása adja át az energiát a levegőnek. Az elektromos szedő esetében a húr transzverz mozgása a mágneses teret modulálja, innentől ez már elektromos jel mindaddig, amíg a hangfal membránja nem csinál belőle újra longitudinális hullámot. A fenti ábrán a baloldali fekete vonal felfogható a hangfal membránjának is. 

Bár a húr és a levegő frekvenciája megegyezik, a hullámhossz és a terjedési sebesség teljesen más a gitárhúr anyagában, mint a levegőben. Pont mint a fénynél. Ráadásul a húr súlya, feszítése is befolyásolja a terjedési sebességet, illetve a hullámok hosszát. Ezért lehetnek, minden húron (az E2-n úgy, mint az E4-en is) ugyanakkora állóhullámok és mégis teljesen más frekvencián rezegnek, más hangot adnak ki. Itt találsz képleteket a húr tömegére, a feszítőerőre és a hullám terjedési sebességére.

Itt meg van egy szimuláció, amit érdemes kipróbálni, mert a személyes tapasztalat többet ér mint ezer szó:

Másik szimuláció. 

Állóhullám a két végén rögzített húron, mindig csak spéci hullámhosszakon (frekvenciákon) alakul ki, és a húron mindig csak egész számú félhullám (orsó) keletkezik. A két végén rögzítést azért rugalmasan kell érteni, ugyanis, ha nagyon bele akarsz merülni, akkor építhetsz is egy ilyen rázókát hangszóróból:

Erre kell rákapcsolni a jelgenerátort, és nyilvánvaló, hogy itt a húr egyik vége fogja betáplálni a rezgést. De ettől még tekinthető fix pontnak. Ekkora hangszórót a telefon direkt módon nem tud meghajtani, erre van ez a kínai bluetoothos erősítő. Szerettünk volna egy sokkal szebb beállítást ahol sötétben fluoreszkáló és foszforos gumit rázunk UV megvilágítással, de a gyenge fény miatt túl nagy macera lett volna. Csak telefonos képeket mutatunk. A legfelső képen a frekvencia 8Hz körül volt, lefelé rendre, 16-24-32-40Hz, vagyis 8Hz egész számú többszörösei. Még egy-két felharmonikus kialakítható, de nagyon lecsökken a madzag amplitúdója, és a hangszórót sem akartuk kinyírni. 

A kísérlet tovább vihető úgy, hogy nem jelgenerátort használunk, hanem egyik végén rögzített húrt, aminek a másik végét súlyok felaggatásával feszítjük ki. Pengetve az alaphangot egy gitárhangolóval mérhetjük a hangolást. Mi a múltkor használt deszkaszterünket alakítjuk át egy csigás súly-felaggatós résszel. És most nem a dualrailt használjuk, hanem egy piezo hangszedőt:

Miket kellene tapasztalnunk?

Ha a húrhosszt duplázzuk a frekvencia feleződik (alsó oktávját kapjuk),
ha a húrhosszt megfelezzük, akkor a frekvencia duplázódni fog (felső oktáv).
Ha a feszítő súlyt négyszeresére növeljük, akkor az alaphang felső oktávját tudjuk kipengetni,
ha a feszítő súlyt negyedeljük, akkor a mélyebb oktávot. 
Ha négyszer akkora tömegű a húr, szintén megfelezi a frekvenciát, 
négyszer könnyebb húr pedig megduplázza azt.

Itt találsz egy kalkulátort, ami az egyes húrokon megadja a szükséges feszítőerőt, pl. a kvint eléréséhez 2.24X nagyobb feszítőerő kell, míg a nagyterchez csak 1,58X. 

A bicikli fékkábel ezennel nem vált be húrnak, 2kg csak 32,5Hz-re tudta kifeszíteni, 8kg megközelítette ugyan a dupláját, de a keskeny spektrum, és a temérdek erős felharmonikus eléggé értékelhetetlenné tette a hangokat. Egy vékony rézdróttal is próbálkoztunk, 500gr súlytól szépen muzsikált, de a 2000gr leszakította. Gyanítjuk, hogy nyúlik is, ezért nem kifejezetten alkalmas erre a kísérletre.

Végül a fékkábelt szálaztuk szét elemi acéldrótra (ez csöppet hullámos maradt kifeszítve is). Igényes kísérlethez mindenképpen egy gitárhúrt javaslunk, amennyiben 500gr és 2kg súlyokat használunk (vizes palackban könnyen kimérhető), mindenképpen a legvékonyabb E4 húrt érdemes kipróbálni (mi sajnáltunk feláldozni egy húrt). Az E4 húrt 25,5-ös skálájú húrhosszon fél kilóval kb. E2-re lehet megfeszíteni, két kilóval E3-ra. 

Érdekesség, hogy egy elektromos gitáron a hat húr kb. 50kg feszítőerőt fejt ki, húronként 8-9kg. Akusztikus gitároknál viszont húronként 11-15 kg is lehet a feszítőerő. Na ezért (is) vágja jobban az ujjakat a dobozgitár húrja.

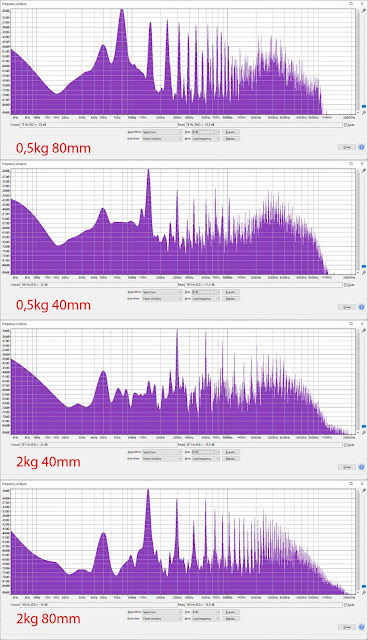
A hullámkép, bár erősen terhelt a felharmonikusokkal, azért valamennyire szemlélteti, amit szerettünk volna.  Körülbelül a D hang néhány oktávját látjuk (és csillió felhangjaikat) a feszítőerőnek és a húrhossznak megfelelően, annyira pontosan, amennyire ez az összedobott berendezés ezt lehetővé teszi. Tehát megfelezve a húrt, kétszeres frekvenciával rezeg, ugyanezt a hatást lehet elérni négyszeres feszítéssel is. 

A hang összetétele folyamatosan változik, tehát nem mindegy, hogy az ábrázolt mintát honnan vesszük a hang elejéről, vagy a végéről, vagy kiátlagolva az egészet (envelope - burkológörbe). A spektogramból kiderül, hogy a mély komponensek lassabban csillapodnak, és minél magasabb egy felharmonikus, annál rövidebb ideig van jelen a hangképben. 

Hasznos linkek:
Húros hangszerek fizikája.
Hanghullám terjedés kalkulátor.