Két a teme, arca csupaszeme. Látható... *

A minap felmerült valami kéklilásan-zöldesen csillogó szemüveg kapcsán, hogy ez meg micsoda. A jelenséggel találkoztunk már a fotóobjektívek, kukkerek fémbevonatainál (amire slendrián módon csak úgy hivatkoztunk, hogy ja igen, az a mágikus Té-réteg). Kicsit utánaolvasva, már nem is biztos, hogy ezek a rétegek csakis fémrétegek lehetnek, sőt. Az egész témakör rokon a vékonyrétegekkel, és a dielektromos bevonatú tükrökkel, vagy micsodákkal (mint például a hotmirror, amit az infrásítás során műtünk ki a fényképezőgépekből, vagy a divatos dikroikus kocka-prizma, vagy interferenciaszűrős nyalábosztó).

A legenda szerint olykor rádióaktív is lehet ez a bevonat, de ezt mások cáfolják, állítólag a rádióaktív lencsékben maga a lencse anyaga tartalmazza a tóriumot (törésmutató növelő hatása miatt) és nem a glazúr. 

Szóval, ez a bevonat, amit nem szabad durva anyagokkal ledörgölni a lencse tisztításakor, mert akkor így fog kinézni, mint ez a szemüveg itt jobbra, nem fogja javítani a képminőséget, oda a kontraszt, a fényerő, meg ilyesmik. Nézd meg a középső képen, hogy ahol a réteg sérült, ott mennyivel több fényt ver vissza az üveg (világosabb a mögötte levő szemüvegkeret feketéje), Szemüvegek esetén kozmetikai hatásnak is hívják, ha nem csillog-villog a lencse, és azért is hasznos, mert emiatt jobb a szemkontaktus. És kevesebb reflexió több átmenő fényt is jelent, de erre mindjárt kitérünk. Mellesleg ezeket már 1886-ban felfedezte Rayleight úr, és mi meg 136 év múlva se értjük. 

Hogyan befolyásolják a visszaverődést a különböző törésmutatók.

Nézzük a normál reflexiót, két közeg határán. Mondjuk levegő-szemüveglencse esetén. Online kalkulátorokat használunk képletek helyett, de azért nesze egy képlet:

Ahol R a reflexió, n meg a levegő illetve az üveg törésmutatója. Visszaverődésre ezt a kalkulátort találtuk. A levegő (n=1) és a koronaüveg (n=1,52) között így alakul a visszaverődés.

Forrás - kalkulátor

Vagyis visszaverődésből van 4% veszteség az első felületen (és 4% a hátsón is). Ez egy szemüveg esetén tűnhet marginálisnak, de mondjuk egy 5-6 lencséből álló objektív esetén már jelentős tényező. 

Nézzük meg, hogyan befolyásolja a visszaverődést a két közeg törésmutatója. Ahogy nő a lencse törésmutatója a levegőjéhez képest, úgy növekszik a visszavert fény aránya is.  n1-n1,52 törésmutatók esetén, mint fennebb láttuk, 4-4% visszaverődésünk van a lencse két oldaláról. A kalkulátor szerint ha gyémántból lenne a lencsénk (n-2,42 törésmutatóval) több, mint 30% visszavert fényünk is lehetne).

Forrás

De mi van, ha a lencse és a levegő közé húzunk egy közbeeső réteget? Mondjuk egy olyat, aminek a törésmutatója a levegő és az üveg törésmutatója közé esik (ideális esetben, akkora a törésmutatója, mint a mögötte levő üveg törésmutatójának a négyzetgyöke, de ennek a miértjét nem firtatjuk, mert sose végzünk hanem). Tehát, ha egy újabb réteget izélünk a lencse elejére, egy kisebb törésmutatójú anyagból, akkor nem 4 visszaverődési felületünk lesz, hanem csak három (levegő-vékonyréteg, vékonyréteg-üveg, üveg-levegő). Ha a lencse hátára is kerül egy ilyen réteg, akkor nem 6 visszaverő felület lesz, hanem 4. 
Nézzük számszerűsítve: levegő-réteg: 1%, réteg-üveg: 1%, és a túlsó oldalon újabb 1-1%. Összesen 4%, vagyis felére csökkenthető a sima üvegfelület két oldaláról visszaverődött fény (vékonyréteg nélkül 8%). 

Az az igazság, hogy kicsivel jobb hatékonyságot vártunk (egy sok lencsetagú objektívnél még ez is rengeteg veszteség és összevissza kószáló fény). Viszont egy kósza ötlettől vezérelve kipróbáltuk, mi van, ha nem egyetlen réteget teszünk a lencsénkre, hanem mondjuk négyet, egytized törésmutatóval növelgetve a rétegeket. Tehát levegő-1,1-1,2-1,3-1,4-1,5, ami az üveg elején 5 visszaverődési pontot jelent, rendre: 0,22-0,19-0,16-0,13-0,12%, ami összesen 0,8%, a lencse hátával együtt is csak 1,6% veszteség visszaverődésből. Na ez már valami, de még mindig nem az igazi.

Hogyan befolyásolja a visszaverődést a destruktív interferencia

A valóságban ennél sokkal jobb átvitelt és még kevesebb visszaverődést lehet elérni (>99%) vékonyrétegekkel. Ugyanis nemcsak a rétegek törésmutatójával lehet bűvészkedni, hanem a rétegek vastagságával is. Kellően vékony vékonyréteg esetén ugyanis a réteg elejéről és hátáról visszavert sugarak interferenciája érvényesül, és ha ez destruktív akkor tükröződésgátló (Anti Reflexion, vagy Anti Glare) réteget kapunk, ha meg konstruktív, akkor tükröt (pl. infrában visszaverő hotmiror). 

Ez a kalkulátor bevezet pár új fogalmat, aztán csiribú-csiribá, kvantum-szórakatémusz és azt mondja a végén, hogy szinte nincs is veszteség az átvitt intenzitásban (transmitted intensity 99.9999%), aztán a visszavert intenzitás meg szinte nincsen is (Reflected  intensity 0.00005%). És mindezt csupán egyetlen réteggel, igaz, ennek annyi a szépséghibája, hogy csak egy adott hullámhosszra ennyire kiváló, de azért a teljes látható tartományon kiváló.

Forrás - kalkulátor 

A rétegnek 1,232 törésmutatót állítottunk be, mert ez lenne az üveg törésmutatójának a négyzetgyöke, ami az optimális törésmutató. A dolog lényege, hogy a visszaverődő sugarak fázisai kioltsák egymást, erre rengeteg magyarázó videó, meg leírás kering a neten. 

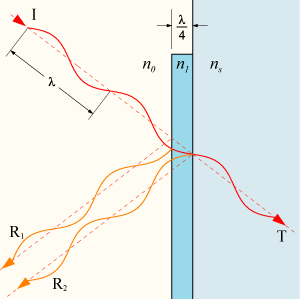Forrás  A hasonló ábrák (rengeteg ilyen van) megtévesztőek,
itt a beesési szög merőleges,
csak valamiért így szokták szemléltetni és elfelejtik említeni.

Ezzel a másik szimulátorral a visszaverődési oldalon a fázisok és interferenciák alakulását lehet nézegetni. FONTOS (mert ez is megzavart minket), hogy az n1,232 törésmutatójú vékonyrétegben az 550 nanométeres zöld fény hullámhossza 446,4nm, tehát ezzel kell számolni ahhoz, hogy a zöld visszaverődését minimalizáljuk, vagyis a vékony rétegünk 112nm vastag kell legyen, hogy a visszaverődő zöld a réteg két oldaláról kioltsa egymást:

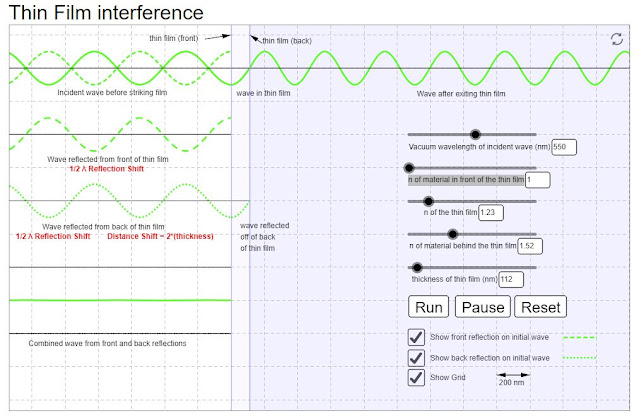Forrás - kalkulátor

A jelenség hasonló lesz a lencse hátoldalán is, amennyiben ott is van egy hasonló réteg, de ott mivel gyorsabb közegbe lépve verődik vissza  fény, se az üveg-vékonyréteg, se a vékonyréteg-levegő határon nem lesz fázistolódás, tehát ugyancsak ellenfázisban leszenek a visszaverődött sugarak. Tehát  lencse anyagában sem fog csomó visszavert fénysugár téblábolni fel és alá, rontva a leképezést.  Az alábbi szimuláció azt mutatja, hogy a lencséből egy vékonyrétegen át, hogyan lép ki a fény a túloldalon. 

De azt, hogy a reflexiós oldalon történő destruktív interferenciától miért lesz a T (transmission) 99,999%, az egyáltalán nem világos. Köze lehet az energiamegmaradásnak, vagyis, hogyha a visszaverődési oldalon hiányzik az energia, akkor az valahol meg kell jelenjen, ha a visszaverődési oldalon destruktív interferencia érvényesül, akkor máshol egy konstruktív interferencia lesz, de nem akarunk úgy csinálni, mintha ezt értenénk. Erre találtunk egy leírást is, de a továbbiakhoz Fressnel úr képleteivel nagyon össze kellene piszkolódnunk és azt sem szeretnénk. Röviden annyi, hogy olyan nincs, hogy az R1 és az R2 kioltják, megsemmisítik egymást. Ami energia hiányzik a visszaverődési oldalon (Ir) az a túloldalon meg fog jelenni (It):

Ha szükséged van egy harmadik nézőpontra is, itt három különböző hullámhosszra szintén találsz egy visszavert illetve átengedett intenzitásmérőt. 

Szimulátor

A wiki szerint a valóságban nem mindig lehet találni olyan vékonyrétegnek való anyagot, aminek a törésmutatója pontosan a bevonni kívánt üveg törésmutatójának a gyöke, elterjedt bevonat például az 1,38-as magnézium-fluorid, és jóvanazúgy, tehát a fenti méregetések pusztán elméleti jellegűek, a technológia lehet teljesen más is.

Na, de mitől vannak a színes tükröződések a lencséken?

Egy zöldre optimizált tükröződésgátló réteg a zöld hullámhosszakat fogja visszaverődéskor kioltani,  nyilván csöppet lilás színben fog visszaverni, mert kevésbé tompítja a vörös és lila hullámhosszakat (?). De ez csak merőlegesen beeső fény esetén igaz, minél laposabb szögben nézzük, a vékonyrétegben annál hosszabb utat tesz meg a fény, tehát óhatatlanul a hosszabb hullámokat fogja jobban kioltani, így előfordulhat olyan szög, amiben a zöld jelenik meg a visszaverődésben. Emiatt lehet egy szemből zöldben visszaverő lencse lapos szögben lilás. 

És lehet több réteget is egymásra halmozni, amivel több hullámhossz visszaverődése is orvosolható. Ezt a megfejtést a többszörös bevonatokkal kapcsolatban, még értelmezni se tudtuk. Ezek után az sem világos, hogy az AR (antireflexió), illetve az AG (antiglare) tényleg ugyanaz a jelenség e. 

A megismerést nagyban megnehezítik a hiányos magyarázatok, a béna, automatikusan magyarított oldalak. Úgyhogy a netről tanulással  csak óvatosan. Mondjuk a legalja ez volt:

Kitalálod mi akar lenni ez a bűnös képlet?

Közben rendeltünk egy dikroikus kocka-prizmát, úgyhogy lehet ha a témára még visszatérünk. Addig is, itt van csomó okosság a metál tükrökről, és ugyaninnen dobbanthatunk a dielektrikum tükrökre. És a szappanyos vékonyrétegek, meg egyéb irizáló dolgok is érdekelnek, szóval lehet ha lesznek még ilyenek is.

* reménytelen