Dehogy a Föld! A pofánk lapos!

Az a helyzet, hogy nincs túl nagy sportértéke a laposföld-hívőkön kacarászni. Leginkább azért nincs, mert a normálisok között is alig találni néhányat, akik igazolni tudnák, hogy a Föld izé..., kerek. Ja nem, gömb! Vagy forgási ellipszoid. Vagyis na, a Föld leginkább geoid alakú... 

- Mi vagy te, tautológus? -  kérdezte Grimpix gúnyosan. 

- Jegyezd meg jól, míg a föld kerek,
   mindig lesznek!  punk's not dead!

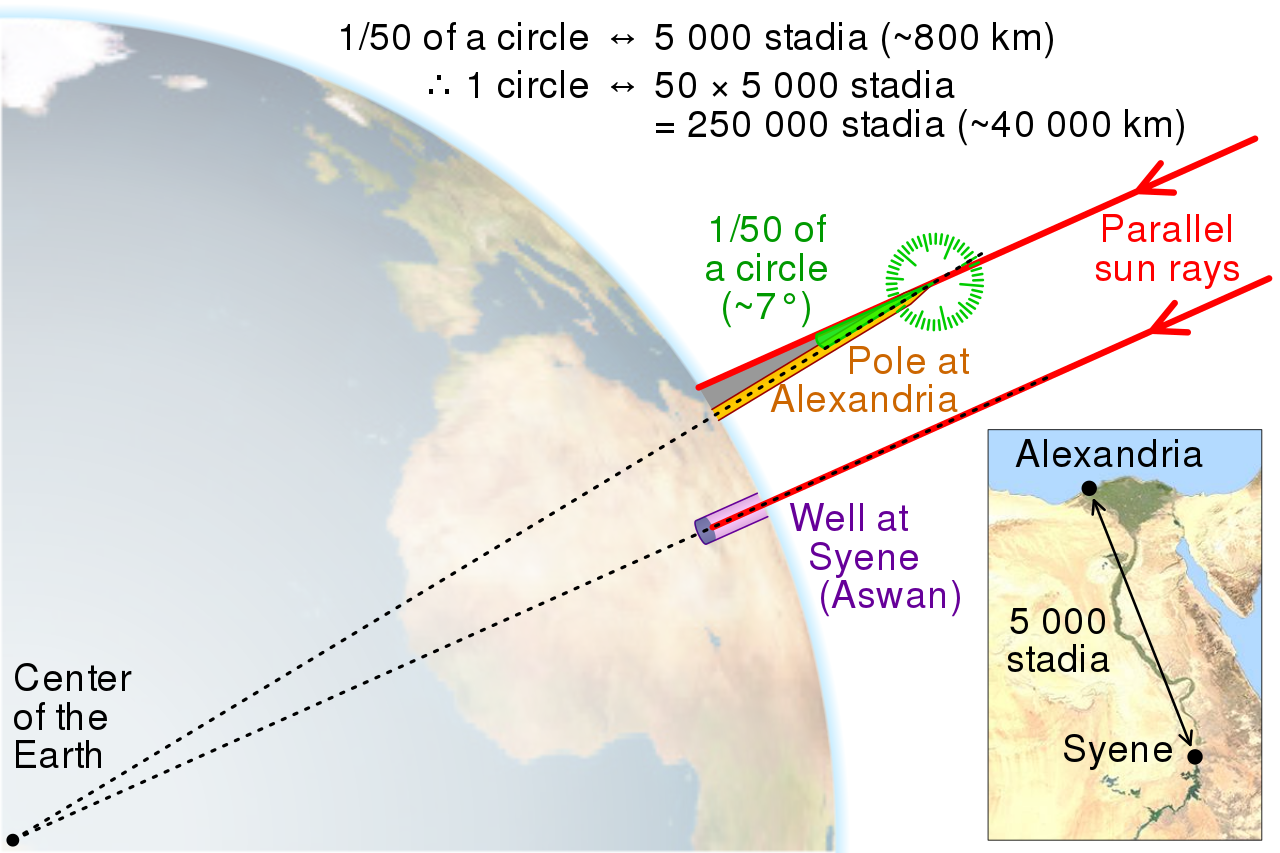
Van ez az egyiptomi szaki, Eratoszthenész, akit tisztelünk, mert nemhogy nem posztolt olyan ostobaságokat, hogy a Föld lapos, de ki is számította a kerületét. De persze, mi, akik nem tudjuk kiszámítani a Föld kerületét (se), ugyanúgy hívők vagyunk, mint a laposföldesek, csak mi  másmilyen óriások vállán állunk, a mi prófétáink, Püthagorasz, Arisztotelész, s nem Rowbotham, vagy kicsoda.

Forrás

Eratoszthenész módszere röviden egy arányszám (nem is maradt fenn a módszere, csak annak egy egyszerűsített változata). A Föld két pontján mért Nap-szögeknek különbsége úgy aránylik a 360 fokos körhöz, mint a két mérési pont közötti távolság a teljes Föld kerületéhez. Másképpen: a Föld kerülete = 360° * a két hely közötti távolság / a két hely napszögeinek különbsége.

A méréshez nem fontos, hogy fixre egy hosszúságon legyenek a mérési pontok (lásd Alexandria és Asszuán), ilyenkor mindkét adott hely delelési maximumakor érdemes mérni, a két pont közötti távot pedig a hosszúság mentén felvenni (nem átlósan). Így egy hosszúsági Föld-kerületet kapunk. 

tangens(Napszög) = rúd hossza / árnyék hossza

Persze az ókori fickóknak nem volt mobiltelefonjuk, hogy egy haverjukkal egyszerre mérjenek árnyékot  messze egymástól, sem repülője, hogy többszáz kilométerre tudjon utazni rövid időn belül, neki ehhez egy Ráktérítő környékére eső pontja volt (ahol a nyári napfordulókor kb. nulla az árnyék és ez az égi esemény szinkronizálta is a két mérést), illetve attól távolabb  egy másik város, ahol árnyékot tudott mérni. 

Az megvan, hogy amikor még nem fénnyel hitelesítettük a métert, úgy definiálták, hogy az egy negyed Földkerület (északtól-egyenlítőig) 10 milliomod része legyen, mert ez megbízhatóbb, mint az inga-méteres? 

Az interneten csomó mindenki elvégezte a mérést, az eredményeik elég vegyesek, ráadásul most nincs se napforduló, se napsütés ami az árnyékhoz elengedhetetlen, se meleg odakint, ezért mi a szobában próbálkozunk. Lássuk jobbak vagyunk e mint ők. Az árnyék méretét a suncalc.org adja meg centi pontosan. Mi se tudnánk ennél szebben mérni. A távolságokat a gugliearthből vesszük, a szögeket meg tangnes inverz kalkulátor segítségével számoljuk. Ilyen cuccai se voltak Eratoszthenésznek. 

- De minek kell ezeket elvégezni, mikor már sokan mások, sokkal pontosabban megmérték? - kérdezte Grimpix. 
- Hát amiért szeretünk hangszeren otthon pötyögni, ahelyett, hogy a csak leghíresebb zenészeket  hallgatnánk, vagy szeretünk a Call of dutyval játszani, mikor nagyapáink már rendesiből megcsinálták a világháborút, vagy amiért kufircolni is szoktunk, holott vannak kaszkadőr úrfik és kaszkadőr lányok, akik sokkal profibban megcsinálták már egymást. - válaszoltam, de mivel Grimpixnek se-füle-se-farka, nem hiszem, hogy értette. 

Na jó, bérmálkozzunk meg tudományos hitünkben, s számoljuk ki a hosszúsági kerületet, ami a wiki szerint 40,007.863 km. A tudományoskodó ismeretterjesztő cikkek és vlogok előszeretettel használják az egyenlítői kerületet (40.075km), ami marhaság, mert a Föld nem szabályos gömb, ezért sokféle kerülete van, de ezzel a módszerrel pont a hosszúságit tudjuk mérni.

Február 16-án Székelyudvarhelyen egy méternek a (legrövidebb) árnyéka 1,63m. Ezzel meg is határoztuk a pozíciónkat szélességen. Tangens függvénnyel (szöggel szembefekvő / szög melletti befogó) ez 58.47°. Válasszunk egy tetszőleges pontot (nagyjából ugyanazon a hosszúságon az egyszerűség kedvéért) és a stílus miatt közel a Ráktérítőhöz. Legyen ez Szudán-Egyiptom-Líbia hármashatára, mert a sivatagban nincs semmi más, amit mérni lehet. Itt az árnyék 0,68m, tehát a Nap beesési szöge (lévén még csak február, nem nulla-közeli az árnyékhossz) 34.21°. A különbség tehát 58,47-34,21= 24,26°. A két hely között 2700,25km a távolság. 

Az aránypár tehát: 24,26° / 360° = 2700,25 / Föld Kerülete. Innen a kerület: 40.069 km. 62 km eltérés a hivatalostól. Azért jók vagyunk, mi? És ki se kellett menni a házból. Mérjünk még egy párat: Székelyudvarhely - Görögország (Imeros beach) 593,65km távolsággal és 1,33 m árnyékkal 39.505 km Grönland alatt az óceánon 39.848 km, a Horn-fok és La Paz között 39.823 km. (Tegnap sikerült 37.500 és 45.500 km között mindent mérni a világ számos pontjai között. Vagy a tegnap hullámzott a Föld, vagy rutint szereztünk a mérésben, de ma sokkal jobbak vagyunk.

Nézzük mik okoznak pontatlanságot, az első mérésre vetítve. 1cm hiba a suncalc árnyékhosszában 300 kilométeres nagyságrendű eltéréseket is okozhat. A távolságmérésben 1km hiba +/-15 kilométeres eltérést eredményez. A szög pontossága is sokat számít, ha 5 tizedes pontossággal számolunk szintén több tíz kilométert okoz a teljes kerületen. Ezeknek a hibáknak a kumulációja okozhat nagyobb eltéréseket, de persze jó esetben tompíthatják egymás hatásait. 

- Na persze, de egy lapos korong alakú Földnek is lehet kerülete - vágott közbe Grimpix. 

Tehát akkor mérjünk egy kerületet másik irányba is. A GoogleEarth segítségével egész jól meg tudtuk közelíteni az elfogadott egyenlítői kerületet: szárazföldön, Afrika leglaposabb részén 40.074,84km (177m hiba), a rosszabb érték 30 kilométerrel volt kevesebb, ezt az óceánon mértük.

Nézzük meg a szélességi fokunk kerületét, ami legyen 46,17°. Mondjuk Székelyudvarhely és Arad között 15 perc van delelési időben (suncalc). Ez 3,75°. Távban pedig 307km. Ebből számítjuk ki: 360*307/3,75, tehát ezen a szélességen a Föld kerülete 29.472km (1° = 81,86km). Összehasonlítva ezzel a jó bonyi  képlettel (vagy a fenti táblázattal), bizony nagy a különbség, ott 27.884km, majdnem 5% hiba, de ebbe belejátszhat az, hogy a 307km távolságot a gugli úgy adja, hogy az összes domboldalt megmássza közben, nem egy referencia ellipszoid mentén.

-Hát ez csodálatos! - mondta Grimpix  - És végül is milyen alakja van a Földnek? - kérdezte - Ha ennyiféle értéket kapunk a szuper programjainkkal, röpködő műholdjainkkal? Milyen alakú a geoid? 

- Leginkább pityóka alakú, azt hiszem. - mondtam és megdöbbenve láttam, hogy Grimpix elégedetten megnyalja a szemét.