Nem túl valószínű, hogy a bárgyú tekintetű, híres szavalóember, 50 cent úr, azért választotta a nevét, mert a negyedhangnak szeretett volna ezzel emléket állítani, szerintünk inkább a erre a dalra rímelhet a neve. A következőben rendhagyó módon, szájbarágósak leszünk, mert ismerkedve a témával ez nekünk gondot okozott, joggal feltételezzük, hogy másnak is gondot okozhat. Tehát úgy közelítjük a témát, like I'm 50.
Osszuk fel frekvencia szerint az oktávot.
Legyen egy (tiszta) oktávunk, amiben 12 félhang távolság van. Hogy miért ennyi, és miért pont ezek, azt most ne firtassuk. Mondjuk ezt teljesen egyformán akarjuk felosztani, a tiszta hangolást érintő problémák miatt. De világos, hogy ez a skála logaritmikus. 110-220Hz egy oktáv, de 220-440Hz is egy oktáv, holott dupla olyan széles frekvenciatartomány, 440-880Hz már négyszer szélesebb, és így tovább.
Mondjuk legyen a felosztani kívánt oktávunk az A4-A5 (440Hz és 880Hz) így van egy 440Hz-es logaritmikus tartomány, ezt kell egyforma tizenkét (fél)hangra bontani. De ezt nem úgy, hogy 440/12 és kész is vagyunk, mert láttuk, hogy mindegyik fél hang egyre nagyobb tartományon fekszik, mint az előző.
Vagyis ez egy mértani sorozat (egy szorzóval növekszik), nem pedig egy számtani sorozat. Az alaphangot, 440-et 1-el szorozva, magát az alaphangot kapjuk. az oktáv esetében az alaphangot 2-vel kell szorozni. Az összes köztes félhang szorzója tehát valahol 1-2 között van.
Oké, tehát keresünk egy olyan számot, ami a 0. hatványon 1 (minden szám ilyen) és ami a 12. hatványon pont 2 lesz, és ezzel a számmal szorozgatjuk végig az azelőtti frekvenciaértéket 12-szer, így lesz meg minden félhangunk frekvenciaértéke.
Ezt a számot meg így kapjuk meg: 12√2 ≈ 1.0594631
Vagyis induljunk A4-től:
440*1,05946 ez lesz az Aisz hangunk 466,16Hz.
466,16*1,05946 lesz a B hang: 493,88Hz
...
és így tovább, míg végül:
Gisz: 830,61*1.05946 ami 880Hz vagyis az A4 hangunk oktávja, az A5.
Vagy másképp megközelítve, a kisszekund (fél hangra a prímtől) 1,05946 szorosa a prímnek. A nagyszekund (két félhangra a prímtől) 1,05946^2 szorosa a prímnek, a kisterc 1,05946^3 szorosa és így fel az oktávig, ami 1,05946^12 szorosa a prímnek, vagyis duplája.
Tegyük fel az A4 (440Hz) kvintje érdekel. A kvint 7 félhangra van az alaphangtól, tehát
1,0594631^7 hatványon * 440Hz = 659.255Hz ami az E5
A wikipedia más megközelítést használ. A képlete:

ahol f(i) a keresett hang frekvenciája, i a két hang közötti félhangtávolságok száma, t0 pedig az alaphang frekvenciája. Lehet a skálán felfele is menni, de lefele is. Most a 440Hz-től induljunk lefele, tehát -7 félhangra (egy kvintnyi távolságra).
f(-7) = 440* 2-7/12 = 440* (1/2)7/12 = 440*0.667419 = 293.664Hz Ez pontosan a D4-es hang frekvenciája (kiegyenlített hangolásnál)
Osszuk fel centekre az oktávot.
Az előbbi számítással a mindennapokban nem lehet együtt élni. Mert az összes hangköz frekvenciaértékeit megjegyezni se lehet, de kiszámolgatni sem életszerű bemindenezve egy koncert közepén. Erre való a cent. A teljes 12 félhangos skála 1200 cent. 100 cent minden egyes félhang. A0 és A#0 között is és A8-A#8 között is, holott az első esetben alig 2Hz (27,50-29,14Hz) a tartomány, a másodikban pedig több, mint 400Hz (7040-7458,5Hz).
Erre léteznek kalkulátorok is, beírod a két frekvenciát és megmondja neked centben a hangközt.
De kiszámolhatod magadnak.
Log kalkulátort is ér használni.
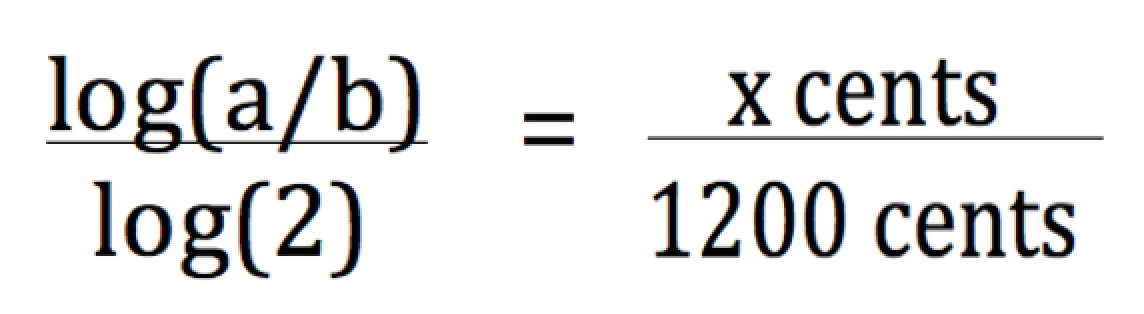
Ahol a/b a keresett hangköz aránya, pl. mint a kvint (3/2), vagy oktáv (2/1). Tehát a 3/2 úgy aránylik a log(2)-höz, mint annak centértéke az 1200 centhez, innen pedig X cent=log(a/b)*1200/log(2), vagyis X cent = log(a/b)* 3986,3137.
Legyen az arány most a tiszta kvart, 4/3 = 1,3333333. log(1,33333) = 0,12493862863, innen 0,12493862863*3986,3137 = 498,04456. Tehát a tiszta kvart hangköz 2 cent híján 500 cent. 2 cent csalás van a tiszta és a temperált (kiegyenlített) hangolás között.
A kvint 3/2 = 1,5 Log(1,5) = 0,17609125905, ez szorozva 3986,3137-tel = 701,95499, 2 centtel több, mint temperált 7 félhang.
Nagyterc (5/4). 386.313712521, itt már azért majdnem 14 cent különbségünk van.
Mi van az oktávval? Aránya 2/1. Érdekesség, hogy bármilyen kalkulációs pontosságot is használunk, az eredmény nem bír 1200 cent lenni (ez a legjobb amit kaptunk: 1,199.9999999826742818476). De persze ez a számítógép pontoss'gi hiányossága lehet (?), hiszen a képlet szerint log(a/b=2)*1200 / log(2), ami log(2)-vel egyszerűsítve tuttifix 1200 kell legyen.
A
wiki más megközelítéseket ajánl, de mostanra mi kielégültünk és elveszítettük az érdeklődést a további hasztalan matematikai maszturbációban.
Azt olvasom, hogy 5 cent fölött kezdik észlelni az emberek a különbséget két hang között, ezt le is teszteltük, 5-10 cent között észleltük mi is az egyszerű szinuszhullám különbségeit. Tehát nekünk a kiegyenlített hangolás pár centes szórása a tiszta hangolástól olyan igazán nagy problémát nem okoz, de elvileg észrevehető számunkra is.

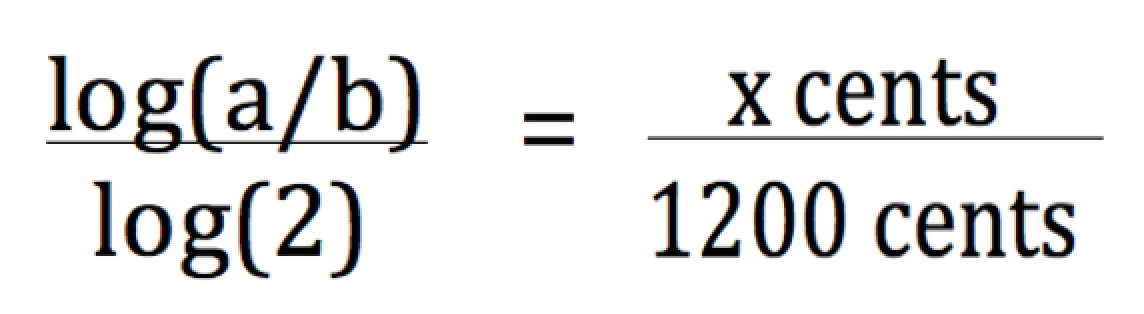
Nincsenek megjegyzések:
Megjegyzés küldése