Az világos, hogy a zene, nem az egyes hangok hangmagasságán alapszik, hanem a hangközökön. Mondjuk, kivéve a White Stripe One note című koncertjét, mert abban a hangköz két performansz közé esik. Annál nem úgy számolunk hangközt, hogy kis- és nagyterc, vagy kis- és nagyszekund, hanem inkább úgy, hogy kiskarácsony, nagykarácsony.
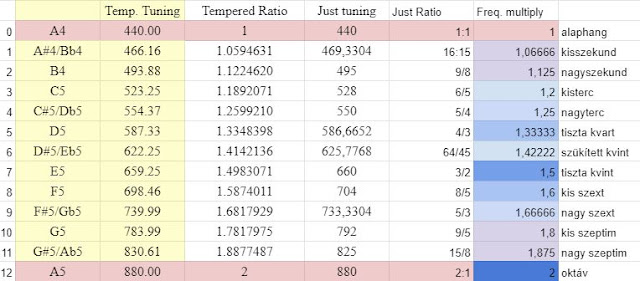
A nyugati zenében a hangközök leírhatók aránypárként, a két hang frekvenciájából. Mondjuk egy kvint hangköz: 3/2 vagyis az alaphang két rezgésideje alatt a kvintje hármat rezdül. Ez eddig ilyen egyszerű.
A4, 440Hz*3/2 = E5, 660Hz (tiszta hangolás esetén). A-nak E a kvintje. De fordítva is igaz A4 440Hz *2/3 = 293.333Hz, ami a D4 hang. Tehát a D4 és A4 között is kvint távolság van, de ezt úgy tanítják a kezdő gitárosnak, hogy D-nek A a kvintje.
Vegyünk most egy másik, cselesebb aránypárt, 5/3. Mondjuk C4 és A4 között. Szext, kilenc félhang. (Kiegyenlített hangolásnál ez 900 cent lenne.) De van egy képletünk, ami két hang arányát megmondja centben: X cent=log(a/b)*1200/log(2), vagyis X cent = log(a/b)* 3986,3137.
a/b helyére behelyettesítve:
5/3 = 884,35 cent (kiegyenlített hangolásnál 900 cent)
10/3 = 2084,35 cent (vagyis 900 cent + egy oktáv, ami 1200 cent)20/3 = 3284,35 cent (vagyis 900 cent + két oktáv, ami 2400 cent)
De másik irányba is igaz:
5/6 = -315,641 cent (vagyis 900 cent - egy oktáv, ami 1200 cent)
5/12 = -1401,577 cent (vagyis 900 cent - két oktáv, ami 2400 cent)
Tehát ezzel a C4-hez képest az A2-A3-A4-A5 hangokat tudtuk megcélozni.
Az előbbi példákban az látszik, hogy a tiszta hangolású aránypárok nem pontosan 100 centre jönnek ki, pl. 884,35 cent a 900 helyett és így tovább. Tehát a tiszta hangolás ezeket a mágikus arányokat használja és fittyet hány a 100 centtel oszthatóságra.
A wiki nem segített megérteni, miért pont ezek a hangközök szerepelnek a ma használt skálában, de fogadjuk el, hogy vannak ezek a történelmileg letisztult, emberi fülnek kedves arányok, amik skálává konszolidálódtak az idők során. Történelmi, fizikai és matematikai okai is vannak, a youtubon sokan magyarázzák, de nem túl meggyőzően. Az alábbi ábra kicsit talán segíthet a hangközök matematikáját megérteni:
 |
| Forrás |
FONTOS, hogy a hangok közötti távolságot úgy adjuk össze, hogy összeszorozzuk az arányokat. Vagyis C-E közötti 5/4f az úgy jön ki, hogy pl. összeszorozzuk a C-D közötti 9/8-at és a D-E közötti 10/9-et. 9/8 * 10/9 = 1,25 ami = 5/4.
Másképpen: a C-A közötti 5/3 arányból ha kivesszük a G-A közötti arányt (10/9), akkor a C-G közötti arányt kapjuk, tehát a törtek osztásával vonjuk ki az arányt: (5/3) / (10/9) = 3/2
Ha pontosan ezeket az arányokat használnánk a hangolásra, akkor tiszta hangolásról beszélhetnénk. A szakirodalom viszont felhívja a figyelmet, hogy ez gondot okozna a zene transzponálása során. Ezt próbáljuk megérteni.
Vagyis ha mondjuk C-ben van a metál és abban reszeljük a kvinteket (C-G), de valamiért ezt át akarjuk tenni D-be, akkor a D-A kvint nem ugyanúgy fog szólni?Az ábra segítségével számoljuk ki C-G között az arány 3/2, vagyis 1,5. De ha összeszorozzuk az egyes lépéseket, akkor szintén: 9/8 * 10/9 * 16/15 * 9/8 = 1,5
261,63*1,5 = 392,445Hz Ez 701,95 cent, ami majdnem 700, mint a kiegyenlített hangolásnál.
De most számoljuk ki ezt D-től kezdve A-ig. Ha a 3/2 aránnyal számolunk, akkor 441,49Hz jönne ki. De ha leszámoljuk a hangközöket 10/9 * 16/15 * 9/8 * 10/9 = 1,48 Így az A hangunk 435,612Hz lenne csak. A hangköz pedig 678,71cent. Ez bő 23 cent különbség C-G és D-A között tiszta hangolás esetén.

Nincsenek megjegyzések:
Megjegyzés küldése