Ha feltételezzük, hogy a Hold annyira közel van hozzánk, hogy a környező csillagok hozzá képest a végtelenben vannak, akkor ugyanabban a pillanatban, a Föld két nagyon távoli pontjáról lefotózva az eget, a környező csillagok eltérő távolságban lesznek a Holdtól a képen. Ha a csillagokat egymásra igazítjuk a két fotón, akkor meg a Hold nem lesz ugyanott a két képen.
A Föld két nagyon távoli pontjáról egyszerre csak úgy készíthetnénk képet a valóságban, ha lennének barátaink Kínában, akikkel ezt megcsinálhatjuk egy összehangolt pillanatban. De nekünk Kínában csak üzletfeleink vannak és azok is egyre kevesebben. Mi a Monncalc.org oldalt használjuk, hogy megkeressük a legközelebbi teliholdat. Jún. 24. éjjelét.
Na jó, a mooncalcon bármelyik napon bármelyik órájára megkapjuk a Hold minden adatát, ezzel a témát le is zárhatnánk, de mi most szimuláljuk a valós kísérletet, így ezeket az adatokat csak ellenőrzésre fogjuk használni. (a Hold 365241km távolságban lesz a Földtől, és aznap 0,547 fokos lesz a mérete).
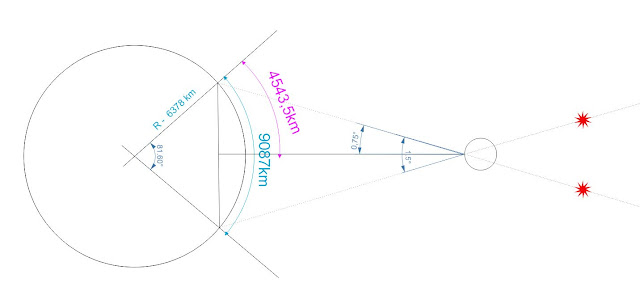
Az időpont tehát adott, ezután a Stellariumban két screencapturet készítünk a választott dátumon, egyidőben, de egyiket Párizsból, a másikat meg a kínai Jiujangból (azt már láttuk, hogy a Stellarium eléggé figyel az apró részletekre). Azért pont ezek lesznek a fotós helyszínek, mert ezek könnyen kiválaszthatók a Stellariumban, plusz egyikből hajnalban, a másikból alkonyat után még éppen látszik a Hold, így majdnem a lehető legnagyobb bázistávolságot kapjuk (9087km).
A két képen a Nyilas-csillagkép nyílhegyének Alnas csillagát, a Kaus Borealist, illetve a Kaus Media csillagokat egymásra igazítjuk. Szemre nagyjából 3 Holdátmérőnyi a parallaxisunk szöge. Tehát nagyjából 1,5 fok felével, 0,75 fokkal kell számolnunk. Keressük meg a szög melletti befogó hosszát, ami a Föld-Hold távolság, ehhez kell a két fotó bázistávolságának a fele.
tan(fél-szög) = fél-bázis / Hold távolsága.
tan(0,75) = 4543,5 / Hold távolsága, ahonnan a Hold távolsága = 4543,5 / 0,013090717 = 347078km
Ami elég szánalmas eredmény.
3. Lehetne valahogy javítani a számításon?
Egyik hiba, hogy a bázis befogója nem 4543,5km, ami a két város gömbfelületen mért távolságának a fele, hanem kevesebb. Reméltük, hogy nem kell ezzel bíbelődni.
A 9087km és a Föld kerületének arányából kiderül, hogy a két mérési pont között (Franciaország és Kína) 81.6 fok van.
sin(40.8fok) = a keresett befogó / átfogó, vagyis a Föld sugara
ami kb 0,64 = befogó / 6378km, ahonnan a pontosabb befogónk 4145km körül van. Sajnos ezzel a pontosítással még távolabb kerülünk a helyes eredménytől, az előbbi tangenses képletünkkel 4145 / 0,013090717 = 316690km Az előbbi eredményünk tehát nem a pontatlan bázistávolság miatt lett pontatlan, hanem annak ellenére.


Nincsenek megjegyzések:
Megjegyzés küldése