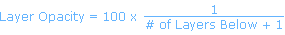Optikai középpont a képek keretezésénél.

A világ bonyolult. Azt hinnéd, hogy a képkeretezésnél a képet középre kell tenni és szevasz, pedig pont nem. Itt olvastunk először róla, nem is tudom, hogy kerülte el eddig a figyelmünket, de még jó, hogy a portfóliónk elkészítése előtt :) ami ugye mindig majd holnap készül, mert van egy olyan indokolatlan illúziónk, hogy örökkétig élünk és ej ráérünk arra még.

Forrás

Ilyesformán kellene kinézzen egy igényes keretezés. És akkor a továbbiakban konkrétan az ablak pozíciójáról van szó. Persze vannak rá szoftverek is, viszont az alábbi könyvrészlet (ezt a könyvet használtuk az Unsharp Mask megértésére is) elég jól megvilágítja a lényeget:

Way Beyond Monochrome Pg. 63.  - Focal Press

A könyv nem foglalkozik szkriptekkel, meg algoritmusokkal, módszere elég egyszerű. A fotót a hordozó bal felső sarkához igazítjuk (A). A maradék területet megfelezzük vízszintesen és függőlegesen egyaránt (a, b vonalak). A fotó bal alsó sarkát (B)összekötjük a O-val jelzett ponttal egy c vonallal, ami így metszi a b vonalat (1). Na ide kell igazítani a print jobb alsó sarkát (C). A harmadik ábra arra az esetre vonatkozik, amikor a keletkezett eredményt túlságosan magasnak találjuk. Ebben az esetben érdemes lecsúsztatni a képet, de nem alább, mint az alsó felezővonal (a) plusz 10%. A könyv szerint ebben a zónában 1-2 a képek zöme jó helyen lesz optikailag.

Persze más forrásokban egészen más megközelítés is lehetséges, befigyelhet csöpp aranymetszés is, de a lényeg azért világos, mindig feljebb kell tenni az ablakot, mint a mértani középpont. És hogy mennyivel? Hát valamennyivel, hogy pont jól nézzen ki.

Custom filter

Nagy csapás az ember számára a rögeszmés működés. Bár  kiút is lehet, egy coping, az intaktság megőrzésére. Szóval nekünk ezért kell kényszeresen egyes körhintáinkon megtennünk néhány kört. Most ez a Custom filter a Photoshopban, amire a kutyának sincs szüksége, nem is értem minek tették bele. Hát hol életszerű, hogy valaki nekilát és ilyen kernel-izé szűrőket kezd fejleszteni? Essünk is hamar túl rajta, mert jobban unom írni, mint te olvasni. Elégtétellel tölt el, hogy még van rajtunk kívül néhány szerencsétlen, aki szintén kényszeresen foglalkozott a témával.

A Custom filter (máshol kernel-szűrő), egy 25-ös mátrixból áll, illetve egy Scale és egy Offset mezőből. A középső pixel kitüntetett, az a mindenkori aktuális pixelünk. A mátrix a körben elhelyezkedő pixelek súlyozását tartalmazza, a scale amennyiben a mezők összegénél kisebb szám, világosítja a pixeleket, amennyiben nagyobb szám, sötétíti (lásd később). Az offset meg egy eltolás, amivel kivédhető egy negatív vagy pozitív túlcsordulás (lásd később), mivel egy pixel értéke se negatív nem lehet sem 255-nél nagyobb. Érdekes, hogy 16 bites kép esetében is nyolc bitesen számol, ami azért gáz, mert a számításokat kerekíti, de így nem használja ki a nagyobb szám adta pontosságot. Ciki.

A Custom Filter a kép minden egyes pixelétét végiglátogatja és az 5*5-ös mátrixot minden pixelre (középre igazítva) kiszámolja, azok minden csatornájára külön-külön. Természetesen egy ideiglenes mátrixba menti az értékeket, tehát mindig az érintetlen képből olvas, a hatás így nem halmozódik pixelről pixelre. Matematikáját egy konkrét szűrő segítségével elemezzük, úgy tűnik ez hiánypótló az interneten (mi innen nyaltuk). És így lehet leginkább megérteni. Ez például egy primitív élesítő szűrő.

A pixelértékek az ábrákon olvashatóak le. A középen levő mályva (vagymiazisten) színű pixel most az éppen aktuális, R csatornájának értéke 111. A képlet meg ez:
(Középső pixel*súlyozása + az akárhány környező pixel*súlyozásukkal) / Scale + Offset
tehát az R csatornát így képezzük:
[(111*15)+(184*-2)+(112*-2)+(123*-2)+(112*-2)] / 7 + 0 = 603/7 = 86 (kerekítve) - és így tovább a G és B csatornákra is.
A környező pixeleket negatív értékkel súlyozva jól látszik az a tendencia, hogy ez a képlet azt eredményezi, hogy a sötétebb pixelek, minél világosabb pixelek veszik körül annál sötétebbek lesznek a szűrő hatására, ugyanakkor a világosabb pixelek meg annál jobban világosodnak, minél sötétebb pixelek veszik körül. Ez a sharpen alapja is, a lokális kontraszt, tehát a tónusok szegélyei mentén, ahol világos és sötét pixelek találkoznak, ott a sötétek sötétednek, a világosak pedig világosodnak, ez fogja az élesség illúzióját adni. Amennyiben az aktuális pixelnél adunk meg negatív értéket, a környezőknek meg pozitívat, ugyancsak élesítés lesz az eredmény, de egyfajta él-kihangsúlyozás is megjelenik.

Gyakorlatilag az történik, hogy az aktuális pixelünk köré kontrasztos hálót rajzol a mátrixnak megfelelően.

Piros mezőben egyetlen bordó pixelre ez az eredmény születik. Ha haránt írunk be értékeket, akkor így módosul a hatás:

Ezzel a mátrixba beírt értékek irányának hatását is szemléltettük. Haladjunk.

Ugyanez a képlet más adatokat beírva a mátrixba okozhat blúrosodást is. Itt egyfajta kiátlagolás történik, tehát a két különböző tónusú pixel tónusa közelíteni fog egymáshoz.

Persze lehet komplexebb szűrőket is építeni, de a kernel mérete sajnos limitált.

A pixel természetesen nem vehet fel akármilyen értéket (0-255), az Offset pont a túlcsordulást kezeli le. A következő szűrő az Invert. Csak az aktuális pixel értékét teszi negatívba, majd ehhez adja az eltolás értékét, jelen esetben 255-öt, ami a szín/tónus inverzét okozza. Például egy vörös pixelnek 255/0/0 az értéke, -255+offset az 0, 0+255 az 255, tehát az eredmény minden csatornán elvégezve 0/255/255 lesz, ami a piros inverze, vagyis a cián szín.

Az offsetet szokták még középszürkére is állítani. Például egy emboss filter esetén.

A mátrix értékeinek összege 0 de a scale csak 1-től felfele vehet fel értéket, emiatt a kép sötét lenne. A +128-as eltolás középszürkére normalizálja a képet. A mátrixban minél nagyobb számokat használunk, annál kontrasztosabb szegélyeket rajzol, a negatív értékű pixel pozíciója meg az árnyékeffektus irányát adja meg.

Sajnos a szűrő működésének megértése nem jelenti azt, hogy most már nagyon fenszi szűrőket is tudunk építeni (itt a kolléga egyszerűtől bonyolultig többféle szűrőt is mutat). Ugyanis egy hangszer működésének ismerete sem jelenti azt, hogy dögös arpeggiókat tudnánk ezáltal komponálni. Ha meg csak az a cél, hogy zenét hallgassunk, akkor arra ugye ott van az Adobe csapatának a szimfonikus zenekara, hogy a képzavart elmélyítsük. Tehát kell egy csöpp kreativitás ehhez az eszközhöz. Mondjuk ez volt az első lépés. Mi itt elengedtük a témát, jobban nem kívánjuk büntetni magunkat. 

Dinamikanövelés kiátlagolással?

A múltkoriban a kiátlagolásra úgy tekintettünk, mint felbontásnövelő lehetőségre. Zajcsökkentésre is alkalmas a kiátlagolás, de ez nem az a technika lesz, amivel a mulatós zajártalmat kell csökkenteni az alsó szomszédból. Arra ugyanis az a jó módszer, hogy a kombót le kell fordítani a padló felé, rá kell dobni néhány pokrócot, aztán bedurrantani a gitárt. Mulatós ellen tökéletes az iszidiszi, díppárpöl, az se baj, ha nem tudsz nagyon zenélni (me Bunyóspityu ért a zenéhez, mi?). Az ájem tíentí, vagy szmókondivóter tökéletesen csiszolja a szomszédok kisgrófón pallérozott zenei ízlését, nem kell értük bonyolultabb arpeggiókat előadni. De ennek a kollégának is remek módszerei vannak.

Hanem arról a zajcsökkentésről lesz szó, amit csillagászok is szoktak használni, vagyis kiátlagolunk több fotót, ezzel a sztochasztikus zaj simán felezhető, negyedelhető és így tovább. Hátránya, hogy csak statikus képekre jó, illetve sok képet kell exponálni, viszont remélhetőleg a tízéves gépünkkel is vállalható zajmentesebb kép lesz az eredmény. És amire leginkább kíváncsiak vagyunk, az a dinamikanövelés. Ugyanis a fotográfiai közhely szerint, ha a zajszintet leszorítjuk, elvileg dinamikát nyerünk az alulexponált részeken. Gyakorlatilag pont ott kellene részleteket nyerjünk, ahol a kép belebukik a zajba.

Az EV a képlet szerint egyenlő log2sqrt(felvételek száma) vagyis 2^EV=sqrt(felvételek száma), amiből az derül ki, hogy 2 fotó esetén csak 0,5 FÉ dinamikát nyerünk, 4 fotó esetén 1FÉ, 8 fotó esetén 1,5FÉ, 16 fotó esetén pedig 2FÉ. Sajnos a képek számának növekedésével nem tart lépést a dinamikanövekedés, mert pl. 64 fotó esetén is még csak 3 FÉ növekményünk van, ami azért már elég abszurd, amikor létezik a HDR technológia, amivel alig 3 felvétellel akár +4FÉ növekményünk is lehet. Na ezért nem használjuk a mindennapi fotográfiában, de annál inkább használják a csillagfotós kollégák. De mi sem használni akarjuk a technikát, hanem csak megismerni.

A fenti kép egy falrészlet, finom textúrája ISO200-on. Teljesen középre exponálva (V. zóna), ahogy a fénymérő látja. Régebbi méréseinknél azt tapasztaltuk, hogy a D5000 kb. -6EV körül bukik bele a zajba, ezért most -8 Fényértékkel készítettünk 16 képet. Így néz ki ezekből egy darab fotó, ACR-ben +5EV korrekcióval, illetve PS-ben még +3EV korrekcióval:

Gyakorlatilag kijelenthető, hogy teljesen bebuknak a részletek a zajba, de azért az látszik, hogy az alacsony frekvenciás részletek (pl. jobboldali vízszintes kiugrás) halványan ugyan, de ott lappanganak. Az apró dudorokat azonban teljesen betemette a zaj.

Egyetlen ilyen zajos képből a Dfine ezt tudja visszahozni:

Azért a nagyobb festékcsomók még ebből a zajos képből is visszajöttek. És akkor ez történik 16 ilyen kép kiátlagolásával (Mean és Median átlagolást próbáltunk, de nem bírtuk eldönteni melyik jobb). Tehát a 16 darab ACR-ben +5EV korrekcióval patkolt képet smart objektumként átlagolva, majd PS-ben újabb +3EV korrekcióval javítva így néz ki:

Nem lett színhelyes, de egészen apró részletek is visszajöttek. Ha figyelembe vesszük, hogy -8fényértékre vagyunk a középső zónánktól, illetve legalább -2 fényértékre a kiexponálható legsötétebb zónánktól, akkor az eredmény egészen jónak tűnik.

Mindenesetre az érdekes, hogy elvileg bár -8 fényértékkel exponáltunk, majd ugyanennyit korrigáltunk, a kiátlagolt képek együtt és külön is jóval sötétebbek  a normál exponálásúnál. Erre majd visszatérünk egy másik bejegyzésben, mert egyelőre nem találjuk az okát, és kísérletet kell szervezni rá. 

Sajnos a tesztfelvételeket slendrián módon elkapkodtuk, ezért nem tudjuk egyértelműen igazolni a fenti képletet, miszerint 16 kép pont 3 fényértéket eredményez. Viszont azt meg tudjuk mutatni, hogy 16 darab -4 fényértékkel alulexponált (majd ACR-ben +4EV-vel korrigált) kép talán mintha egy hangyányival gyöngébb lenne, mint a normálisan középre (V. zóna) lőtt kép.

Régebb, a smart objektumok kora előtt a felvételeket egymás fölé kellett rétegelni és az átlátszóságot az alábbi formula szerint kellett beállítani minden rétegre:

Forrás

Amúgy a módszer alkalmas az otthon felejtett ND szűrő helyettesítésére is. Sok rövidebb exponálást lehet vele egy hosszúba olvasztani.

Miért van kétszer annyi zöld pixelünk?

Persze, mert a szem érzékenyebb a zöldre? Hogy is van ez? Meg aztán nem az van, hogy a demozaik úgyis egységesen interpolálja a színeket? Végül úgyis 12 megapixel zöldet, pirosat és kéket kapunk a szemünkbe. És vannak teljesen más színbontású szenzorok is, ahol a zöldnek cseppet sincs kitüntetett szerepe. Azokkal mi van?

Leginkább arra hajlunk, hogy ha már 3 színre bontott szenzort kell használni (festékek előállítása, CFA kialakítás technológiája, gyakorlatba ültethető színelmélet miatt), azt legegyszerűbb úgy elosztani, hogy egyik pixelből kétszer annyi lesz. És akkor már érdemesebb ha pont a zöldből van kétszer annyi, hiszen a szem leginkább (?) a zöld hullámhosszak által hordozott luminancia változásaira a legérzékenyebb. Azt már láttuk, hogy a kontraszt, vagy fényesség érzékelésünk jobb, mint a színérzékelésünk, és hogyha a világban is a zöldben látunk legtöbb részletet, akkor dupla zöld pixelből pontosabb és zajmentesebb luminanciaérzetet tudnak kiváltani, vagyis jobb fényesség felbontást. A színérzékelés kiváltására a pontatlanabb R illetve B interpolációja is megfelel. 

Baloldalt az egyesített piros-kék csatorna, a jobboldali pedig a full zöld. 

Teljes nagyításban nézzétek a képeket. Olyat is olvastunk, hogy a zöld luminancia-felbontása még a piros-kék csatornák összesített luminancia-felbontását is megverik. Ezt nem teljesen értjük, viszont a kísérlet alátámasztani látszik ezt is.