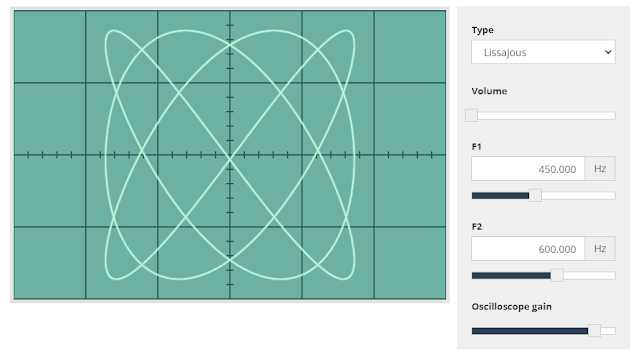
Pár dolog még bennünk maradt az oszcilloszkópos rajzolgatással kapcsolatban. Lissajous-görbéket régebb rajzoltunk Y ingával is (blackburn-inga), ami jó móka, csak kevésbé kontrollálható, mint egy szimulátor:
 |
| Forrás |
Ez sajnos nem tud fázist állítani a két frekvencián. Viszont tud a Wolfram playerre letölthető, vagy ennek online cucca. A wolframos cucc fáziseltolását Pi-ben kell megadni (vagy radiánban), így a 180 fok Pi, a 45 fok Pi/4, stb.
Az x:y=1:1 arányra minden remekül összevág (SoundcardOscilloscope-pal csekkoljuk, plusz Lissajous táblázatot is figyeljük):
Az x:y=1:1 arányra minden remekül összevág (SoundcardOscilloscope-pal csekkoljuk, plusz Lissajous táblázatot is figyeljük):
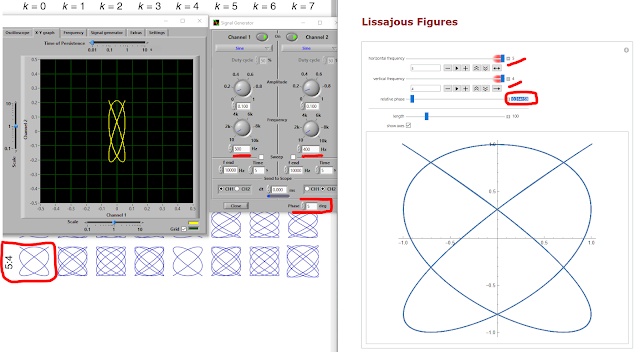
Aztán ahogy haladunk a bonyolultabb arányok felé, egyre inkább a három háromfélét mutat.
Ahhoz, hogy az ábrának megfelelő alakzatot kapjunk, az oszcillátoron 5 fokos fáziseltolás kell, a Wolfram-szimulátorban pedig 0,3 rad, vagyis kb. 17 fok. Az okához kevesek vagyunk, de biztosan van rá tudományos magyarázat.
 |
| Emlékeztető |
A következő szimulátorban mindkét tengely fázisa állítható, ez nagyjából ugyanaz a műszer amit a sztereó-két hangszórója derékszögben hajt meg.
 |
| Forrás |
Még adtunk egy utolsó esélyt a hangfalmembránra ragasztott tükörnek is, valami hasonló setuppal, mint ebben a videóban, csak nekünk folpack volt a membránunk és a tükör is egy darabka normál tükör, ami pár grammos lévén azért eléggé meghatározta, hogy milyen mozgásokra képes. Magas frekvenciákat nem is lehetett megjeleníteni vele.
Érdekesség, hogyha csak egyetlen frekvenciát tolunk bele, akkor szabályosabb ábrát rajzol, ha kettőt, akkor a lebegés miatt el-elszabadul. Gyanítjuk azért, mert közben a spektrum érinti a rendszer rezonanciafrekvenciáját, amitől pillanatra elszabadulnak az indulatok, aztán ahogy kiesik a fázisból hamar lecseng a dolog. Ezt igazoltuk azzal, hogy egy alapfrekvencia mellé (pl. 10Hz) egy másikat engedtünk, amit finoman növeltünk (10-100Hz között). Észleltünk valamiféle mintázatot a nagyamplitúdós rezgesek eloszlásában, de annyira szedett-vedett ez a beállítás, hogy nem akarunk mélyen belemenni, csak elengedni végre ezt a dolgot.




Nincsenek megjegyzések:
Megjegyzés küldése